此前我们讨论了和期权隐含波动率相关的一些分析指标，如相同期限相同档位下的认沽期权与认购期权的隐含波动率差衡量了市场对标的在未来特定日期运行到特定价格上（下）的预期强弱差，也就是在特定价格上看涨和看跌的市场预期差。另外在相同期限不同档位的认沽（或认购）期权隐含波动率形态反映了市场对标的在未来特定日期运行到不同价格区间之下（或之上）的预期强弱，且我们发现由于实际市场中暴涨暴跌极端收益率相对肥尾的分布特性以及流动性的问题，此形态通常呈现两端翘曲的“微笑结构”（Smile）或被某一段时期市场情绪所主导的偏斜结构（Skew）。

上面这些和波动率相关的指标都是针对具有相同行权日期的认沽认购期权而言，他们均衡量了市场对于标的在未来 某个固定日期 运行至各价格区间的预期强弱大小。而我们知道实际在市场上交易的还有各种不同剩余期限（行权日）的期权，那么接下来我们就将讨论具有不同行权日的期权隐含波动率的结构及其的一些分析与应用。

Volatility Term Structure，期权波动率期限结构

从字面理解，波动率期限结构就是认沽或认购期权在（相同档位），不同行权日期下隐含波动率的取值分布以及顺次差值。类似于我们研究相同期限下不同档位的期权波动率曲线形态，我们也可以研究相同档位下不同期限的期权的隐含波动率曲线形态。

下面两幅图分别是2020年2月18日上午50ETF期权各档位认购和认沽波动率期限结构（M0代指当月合约，M1代指下月合约，M3、M6、M9分别代指后面的季月合约）：

2020.02.18日50ETF认购波动率期限结构：

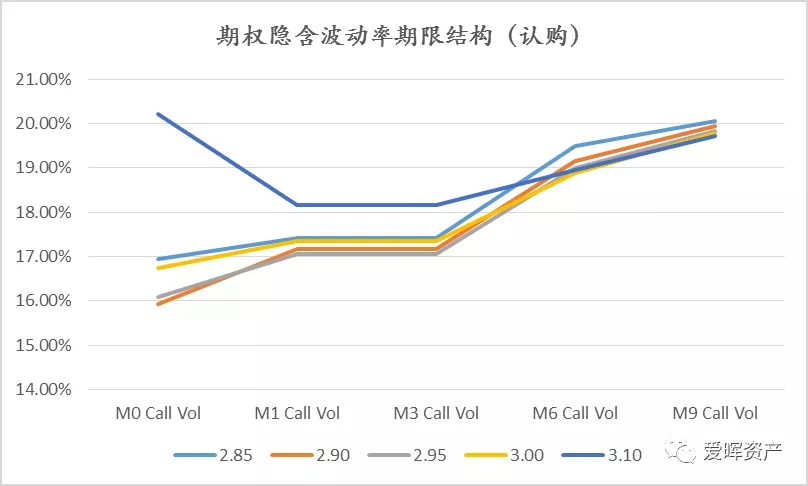
2020.02.18日50ETF认沽波动率期限结构：

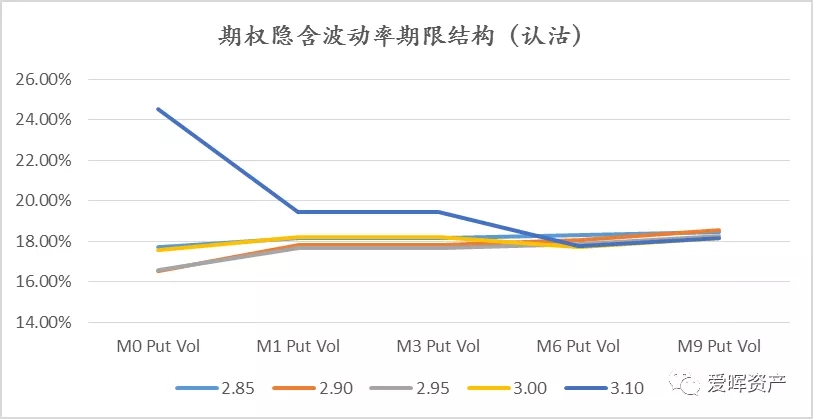
我们看到，即使对于相同档位，具有不同到期期限的期权合约的隐含波动率取值也可以是相差较大的。以平值为例，上图中认购曲线里隐含波动率最高的期限为9月合约，取值达到了20.15%，而最低的隐含波动率期限为2月当月，取值近为16.33%，同一时间两者差异有近4个百分点。而认沽曲线则相对平滑很多，平值档位隐含波动率最高的期限也是9月合约，取值18.26%，最低的期限也是2月当月，取值16.54%，两者差异不到2个百分点。

而从期权隐含波动率期限结构曲线的形态上来看，除开和目前平值（2.95）偏离较远的3.10档位，各个档位的期限曲线走势是大致相似的。另外，相较于当月到期的期权，远期合约中相同期限下不同档位的认沽或认购隐含波动率差异也显著较小（实际上，这里描述的是不同期限合约下的微笑或偏斜结构）。

如之前所说的，现实中每个期权的“波动率”σ ，都是根据人们对该期权的交易需求，由其在市场上实际交易出来的价格反向推算而得的“隐含取值”。其相较于实际波动率的折价或溢价，也代表了市场对于标的未来价格运行区间的预期强弱。所谓的期权波动率期限结构，相同档位下各个期限期权隐含波动率数值的不同，就是由市场对于标的在未来不同时间（行权日）运行到既定价格（档位）上下预期强弱交易而得的。

相对来说，当月期权和次月的期权合约一直存在且交易最为活跃，其隐含波动率的差值根据人们对于近远期标的价格运行至某一区间预期强弱的变化反应也最为敏感。我们以滚动平值档位的当月期权隐含波动率（认沽认购加权平均）与次月期权隐含波动率的差值为例，看看近远月期限结构分布情况：

50ETF与滚动平值近次月隐含波动率差值：

从分布上来看，近次月隐含波动率的差值是较为均匀和对称的（略微偏左）：

50ETF滚动平值近次月隐含波动率差值分布：

类似于我们研究相同期限下认沽认购平值波动率差与标的走势的关系，我们再来看看滚动平值近次月波动率差与50ETF的走势之间有怎样的联系。由于直接取近次月隐含波动率差毛刺较多（一个原因为平值档位的频繁游走与日内波动率价格的随机波动），我们用其20日EMA均线来描述其趋势性变化：

50ETF与滚动平值近次月隐含波动率差值20日EMA：

从上图中我们同样可以看到标的与近次月波动率差的趋势性变化之间存在较为显著的“镜面对称的”负相关关系：标的的趋势性上涨（或下跌）一般伴随着平值近次月波动率差的趋势性下降（或上升），而平值近次月波动率差的阶段性见底（或见顶）结合标的高位阶段性见顶（或见底）一般也预示着拐点信号的到来。

No.2

波动率期限套利的机会

从上面平值近次月波动率差的分布我们可以看到，整体而言代表期限结构的差值是在一定范围内变化的，当差值达到历史分布较大或较低水平时，理论上均可以做期限结构在逆向方向的回归套利。我们这里做一个简单地测试：

当Vol Gap超过历史分布85%分位值时，尝试做空差值，实际操作中选取当月平值跨式组合卖出（卖出相同数量的平值认沽与认购期权），远月平值跨式组合买入（买入相同数量的平值认沽与认购期权），同时对剩余 微弱 delta用50ETF进行对冲（实际上由于大部分时间剩余delta较小近似为零，也可以不做对冲）。在Vol Gap下降至历史35%分位以下认为套利逻辑兑现，平仓。反之，当Vol Gap低于历史分布15%分位值时，尝试做多差值，实际操作中选取当月平值跨式组合买入，远月平值跨市组合卖出，剩余delta利用50ETF对冲，在Vol Gap上行至历史65%分位以下认为套利逻辑兑现，平仓。

策略从2016年年中开始日频执行。不计滑点与手续费，年化收益率为10.83%，期间最大回撤-3.48%：

波动率期限套利（50ETF对冲）：

如剩余delta不做对冲，不计滑点与手续费，年化收益率为10.21%，期间最大回撤-4.59%：

波动率期限套利（50ETF对冲）：

- The End -

本文仅供参考，投资有风险

请投资者自行判断投资机会并承担投资风险

爱晖资产

专注于量化领域的证券基金资产管理公司